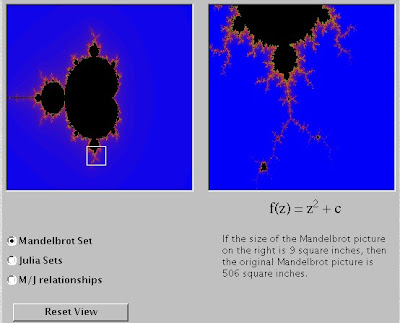
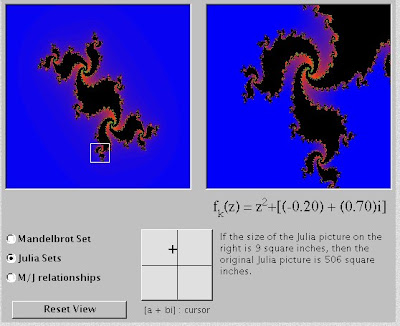
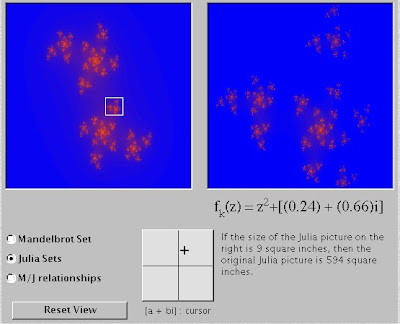
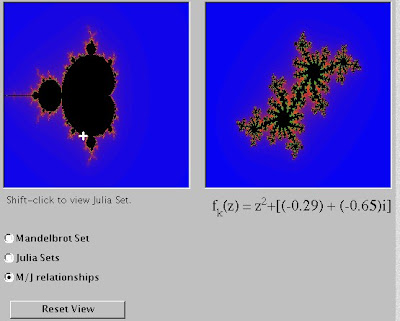
Of David.
1 Oh, hai! CEILING CAT is my cheezburgr.
who i iz scard of?
CEILING CAT is my kitteh bed—
who i iz scard of ffs?
2 Wen skript kidehs DOS me
to nok me offline
when trols n lusers atak me w/ teh BFG,
tehy wil trip on it.
3 If a crew raid me,
I not chikn;
even if tehy stole my bike,
i stil rulz!
4 One thing I askz 4, O CEILING CAT, plz,
this is what I luk 4. Ready?:
cheezburgrz
evry dai, srsly,
yumy laik CEILING CAT's beleh fuz
cuz cheezburgrz bring me closer 2 u kthx.
5 For wehn Brian Peppers cums 4 me
CEILING CAT keepz me sayf;
he hidez me in his tabby-nacle
n putz me on top of book shelf.
6 Then i iz lookz down on nmes
above the nmes taht suround me;
at his tabby-nacle I will sacrifice a mouse w00t!;
I will sing "We Are teh Champyons" 4 CEILING CAT.
7 Hear me meow, O CEILING CAT,
DO NOT WANT u 2 pwn me. Hit me up on mesenger plz.
8 I getz feelin i sposed 2 fynd ur fuz face r sumptin,
Ur fuz face, CEILING CAT, I luks 4.
9 No hydz ur fuz face frm me plz,
no get pised of @ me plz;
cuz u hav helpd me ffs.
no putz me on ignor list,
O CEILING CAT.
10 Even if mom n dad kill filter me,
CEILING CAT wil readz al my emailz.
11 Teach me skilz, O CEILING CAT;
show me how 2 pwn
skript kidehs.
12 Do not giv tehm r00t on my servr,
cuz tehy sez tehy pwn me already ffs,
ther breath stinkz of hot pokets n diet pepsi.
13 Im shur:
I wil seez teh fuzy beleh of CEILING CAT
b4 I diez.
14 Wait for CEILING CAT;
hez comin srsly
wait for CEILING CAT kthx bai.
1 Corinthians 1:10-18
Divisions in the Ceiling Cat Clubz10 Evribodi get along plz?
11 bcz Chloe telled on u! OMG u r fightin!
12 I iz tryin sai: one d00d sez "me follaz Paul"; differnt d00d sez "me follaz Apollos"; third sez "me follaz Cephas"; An sum othr d00d "me follaz Christ!" Srsly WTFBBQ!
13 Christ iznt in bite-size chunx! Is Paul on cross for u? NO! U wuz givn bath for Paul? NO and also OMG waterz!
14 I iz glad I not gived u bath! (xcept Crispus An Gaius)
15 so nobodi can sez anybodi gotted bath in mai namez (xcept Crispus An Gaius).
16 (OK I gived Stephanas An his families bath. N maybi some1 else, I forgets.)
17 enniwai Christ didn't sended me to giv u bath! He sended me 4 telling you good newses about Ceiling Cat! An I duz not do that wif smart human wordz! Bcz that meanz Christ's cross haz no powerz! oh noes!!!
Ceiling Cat iz Smartr than U18 Msg 4m cross 2 teh dyin: i iz just silly. msg 4m cross 2 us who iz being savedz: i iz the powr of Ceiling Cat!
Matthew 4:12-23
Jesuz begunz 2 preech, amirite?12 Wen Jesus founded out dat John wuz in prison he made tracks fr Galile
13 An staid in Capernaum at teh c-side bt he dint tak his bukkit an spayd.
14 Cuz teh wize Esaias sed
15 “In all teh base, laik Zabulon n Nepthalim n teh c n Jordan (yeh even KT Prys) n Galilee.
16 Jesus will turn on teh liteswitch fr teh kittenz dat iz sittin in teh dark."
17 Dat iz wen Jesus strted 2 tell teh kittenz, “repent cuz teh kngdom of heaven am at hand btw.”
The callin of teh frist desipels18 Den Jesus bumpded into 2 broz hoo wuz fisherzmen n wuz called Simon AKA Peter n Andrew AKA Lil’ Bro
19 N Jesus sed, “Comes wit me n u can b manfisherz.”
20 N cuz Jesus am teh 1337, dey wuz laik, “kthx.”
21 N den Jesus met James n John, hoo wuz chillin on a bote wit dair pops, hoo wuz Zebedee frm teh Magic Roundabout.
22 N dey also went wit Jesus.
Jesuz heels teh sIckly23 Jesus tuk hs crew roun Galilee, teechin in teh tmples n preechin teh gospel n heelin teh sick.
We hope to have many other Holy Kitties featured this year.
 One of the red squirrels moved into the garage for the winter. Amelia didn't like that. It was in the ceiling of one of the rooms in the house and in the attic. A squirrel has moved in every winter and I didn't know what the problem was (oh, Amy told me what the problem was). The dogs go nuts in the garage trying to track the squirrel, and the last insult was when it stole and chewed a pack of cigarettes. I became worried about squirrels smoking in the house, so I agreed that Amy could try to trap it in my havahart trap. Twice, the squirrel retrieved the peanut butter bread and closed the trap but never was itself trapped. The third time was the charm. Today, my little squirrel was safe inside the trap.
One of the red squirrels moved into the garage for the winter. Amelia didn't like that. It was in the ceiling of one of the rooms in the house and in the attic. A squirrel has moved in every winter and I didn't know what the problem was (oh, Amy told me what the problem was). The dogs go nuts in the garage trying to track the squirrel, and the last insult was when it stole and chewed a pack of cigarettes. I became worried about squirrels smoking in the house, so I agreed that Amy could try to trap it in my havahart trap. Twice, the squirrel retrieved the peanut butter bread and closed the trap but never was itself trapped. The third time was the charm. Today, my little squirrel was safe inside the trap. Here is the little rascal patrolling her snow tunnels in the back (taken through window). I'm taking bets on how long it will take her to move back into the house.
Here is the little rascal patrolling her snow tunnels in the back (taken through window). I'm taking bets on how long it will take her to move back into the house.